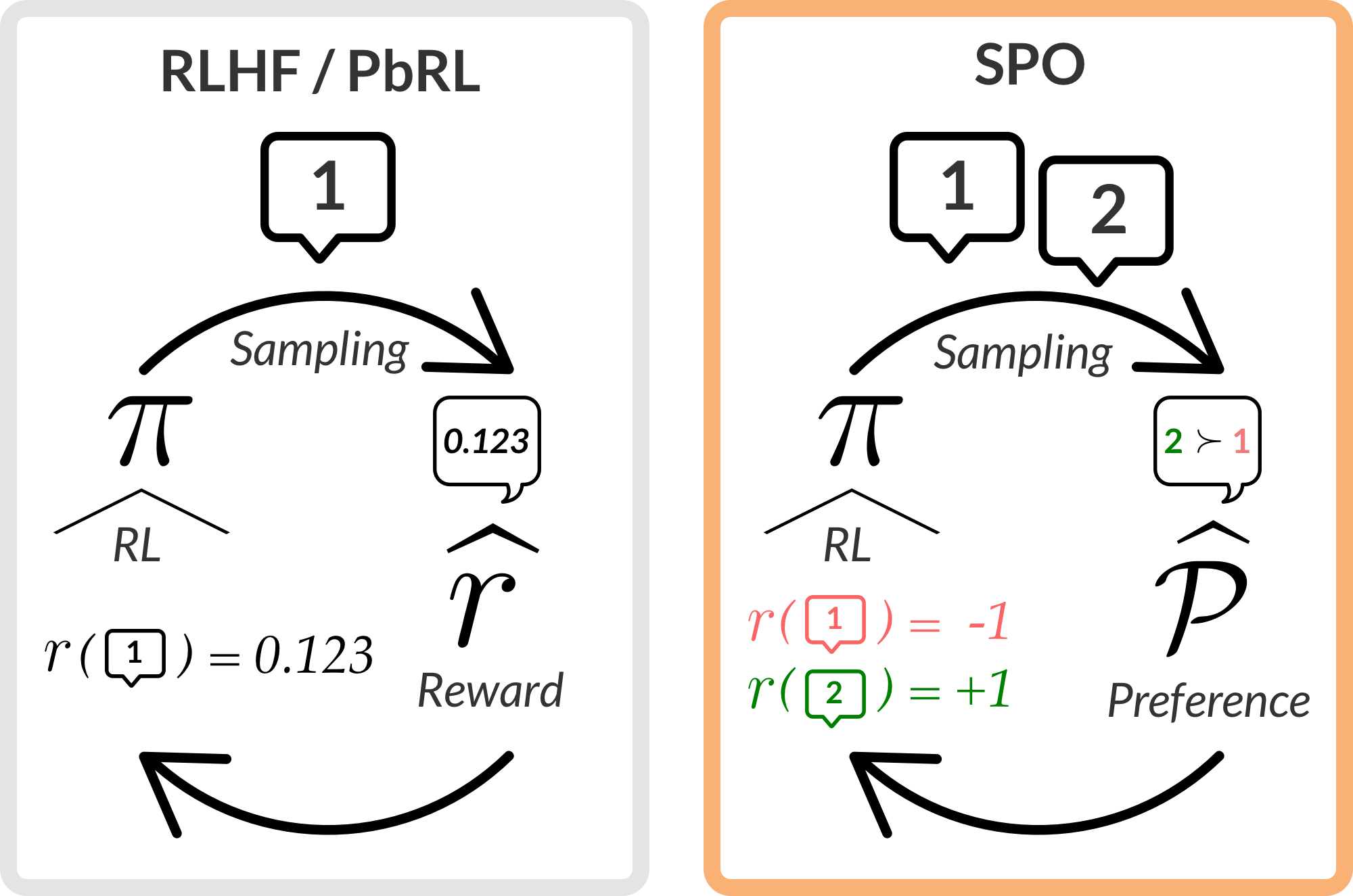
TL;DR: Reward-based approaches to RLHF struggle to robustly handle diverse rater preferences as they attempt to rationalize them with a single reward function. We propose Self-Play Preference Optimization ($\texttt{SPO}$), a scalable algorithmic framework to rigorously address this issue by fusing insights from game and social choice theory. Practically, $\texttt{SPO}$ corresponds to sampling multiple trajectories from a policy, asking a preference or teacher model to compare them, and then using the proportion of wins as the reward for a particular trajectory for a downstream policy optimization algorithm.

Abstract

We present Self-Play Preference Optimization ($\texttt{SPO}$), an algorithm for reinforcement learning from human feedback. Our approach is minimalist in that it does not require training a reward model nor unstable adversarial training and is therefore rather simple to implement. Our approach is maximalist in that it provably handles non-Markovian, intransitive, and stochastic preferences while being robust to the compounding errors that plague offline approaches to sequential prediction. To achieve the preceding qualities, we build upon the concept of a Minimax Winner (MW), a notion of preference aggregation from the social choice theory literature that frames learning from preferences as a zero-sum game between two policies. By leveraging the symmetry of this game, we prove that rather than using the traditional technique of dueling two policies to compute the MW, we can simply have a single agent play against itself while maintaining strong convergence guarantees. Practically, this corresponds to sampling multiple trajectories from a policy, asking a preference or teacher model to compare them, and then using the proportion of wins as the reward for a particular trajectory. We demonstrate that on a suite of continuous control tasks, we are able to learn significantly more efficiently than reward-model based approaches while maintaining robustness to the intransitive and stochastic preferences that frequently occur in practice when aggregating human judgments.

Video

Key Insights

1. Aggregating Diverse Rater Preferences Produces Intransitivity

Consider aggregating (as is neccesary at scale) the population of three raters, each of whom has rational preferences (i.e. preferences that can be explained by a reward / utility function).

Observe that there is no utility function that can rationalize these aggregate preferences as it would need to score 🪨 over ✂️, ✂️ over 📝, and 📝 over 🪨, an impossibility. This problem only becomes worse when raters have more options to chose between (e.g. the space of all natural language completions to a prompt). As a result, reward-based RLHF methods (PPO, DPO) will attempt to satisfy the majority preference, ignoring the diversity of preferences actually present in the rater population.

2. Framing RLHF as a Game

Thankfully, social choice theorists have been thinking about the problem of preference aggregation for a long time. A classical solution concept is the minimax winner, which proposes framing learning from preferences as solving a two-player zero sum game: $$p^*, q^* = \arg\min_{p \in \Pi} \arg\max_{q \in \Pi} \mathbb{E}_{\xi_1 \sim p, \xi_2 \sim q}[P(\xi_1 \succ \xi_2)],$$ where $P$ is a learned preference or teacher model. Intuitively, both players ($p$ and $q$) are trying to generate prompt completions ($\xi_1$ and $\xi_2$) that are preferred to those of the other player. Critically, because we are not collapsing down the preference matrix to a scalar reward, we are agnostic to whether intransitive preferences exist. Unfortunately, solving this game via adversarial training is infeasible at the scale of modern-day LLMs.

3. $\texttt{SPO}$: Self-Play Preference Optimization

Observe that the above game is perfectly symmetric (i.e. $p$ and $q$ swapping strategies leads to the same payoff). Thus, rather than maintaining two policies in memory, one can instead adopt a simple self-play strategy of just comparing multiple completions from the same policy while preserving strong theoretical guarantees.

Main Theorem (Informal): Define the following sequence of policy-dependent $\texttt{SPO}$ rewards: $$r_{t}^{\texttt{SPO}}(\xi) \triangleq \mathbb{E}_{\xi' \sim p_t}[P(\xi \succ \xi')].$$ Let $\mathbb{A}$ be a no-regret algorithm over the policy class. Set $p_{t+1} = \mathbb{A}(r_{1:t}^{\texttt{SPO}})$. Then, the average policy $\bar{p} = (p_1+\ldots+p_T)/T$ is an $\frac{2 \mathsf{Reg}_{\mathbb{A}}(T)}{T}$-approximate Minimax Winner.

This is a general reduction from computing Minimax Winners to no-regret online learning!

Practically, $\texttt{SPO}$ corresponds to sampling multiple trajectories from a policy, asking a preference or teacher model to compare them, and then using the proportion of wins as the reward for a particular trajectory for a downstream policy optimization algorithm.

Paper

@misc{swamy2024minimaximalist,
    title = {A Minimaximalist Approach to Reinforcement Learning from Human Feedback},
    author = {Gokul Swamy and Christoph Dann and Rahul Kidambi and Zhiwei Steven Wu and Alekh Agarwal},
    year = {2024},
    booktitle = {Proceedings of the 41st International Conference on Machine Learning}
}

Acknowledgements

This template was originally made by Phillip Isola and Richard Zhang for a colorful ECCV project, and adapted to be mobile responsive by Jason Zhang. The code we built on can be found here.